Introduction to Stochastic Analysis: Integrals and Differential Equations

Chapter 6

Stochastic Differential Equations

 

 

Now, we can already make sense of the integral equation

[6.1]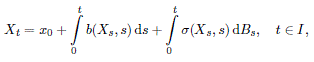

derived in Chapter 3 (most often, I = [0,T] or [0, ∞)). Though partially for historical reasons, but rather for practical convenience, it is usually written in the formal differential form

[6.2]

Both equations are called stochastic differential equations, though here the word integral would fit better. A formal definition is as follows.

DEFINITION 6.1.– A continuous random process X_t, t ∈ I, is a solution of the stochastic differential equation [6.2] in an interval I if for all t ∈ I, it satisfies equation [6.1] with probability one.

EXAMPLE 6.2.- Consider the stochastic differential equation

This equation describes, for example, the dynamics of stock price in financial mathematics, or the development of some populations in biology. Let us check that the random process X_t = x₀ exp{(µ−σ² /2)t+σB_t}, t 0, is its solution. Applying the Itô rule (Theorem 5.2) to the function F(t, x) = _x exp {(µ − σ²/2)t + σx},we have:

In particular, for µ = 0 and σ = 1, we get that the random process ...