2
Mathematical Description of Random Signals
The concept of frequency spectrum is familiar from elementary physics, and so it might seem appropriate to begin our discussion of noise like signals with their spectral description. This approach, while intuitively appealing, leads to all sorts of difficulties. The only really careful way to describe noise is to begin with a probabilistic description and then proceed to derive the associated spectral characteristics from the probabilistic model. We now proceed toward this end.
2.1 CONCEPT OF A RANDOM PROCESS
We should begin by distinguishing between deterministic and random signals. Usually, the signals being considered here will represent some physical quantity such as voltage, current, distance, temperature, and so forth. Thus, they are real variables. Also, time will usually be the independent variable, although this does not necessarily need to be the case. A signal is said to be deterministic if it is exactly predictable for the time span of interest. Examples would be
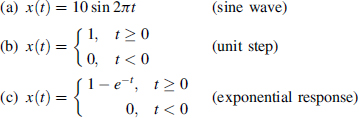
Notice that there is nothing “chancy” about any of these signals. They are described by functions in the usual mathematical sense; that is, specify a numerical value of t and the corresponding value of x is determined. We are usually able to write the functional relationship between x and t explicitly. However, this is not really necessary. All that is needed is to ...
Get Introduction to Random Signals and Applied Kalman Filtering with Matlab Exercises, 4th Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

