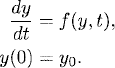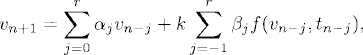Introduction to Numerical Methods for Time Dependent Differential Equations

CHAPTER 5

TWO-STEP AND MULTISTEP METHODS

The character of some equations, such as the equations of motion in a many-body problem in Newtonian mechanics, requires methods of high and very high orders of accuracy. The use of high-order one-step methods (such as Runge-Kutta methods) for such problems turns out to be computationally very expensive. For this reason multistep methods have been developed. These methods can be both of very high accuracy and fast. In this chapter we study the leapfrog method, which is the simplest of all, and Adams methods, which include both explicit and implicit methods. At the end we show a simple example of the predictor-corrector strategy for multistep methods.

5.1 Multistep methods

Consider the initial value problem

(5.1)

Thus far, we have approximated equation (5.1) by one-step methods (see Definition 2.9). They have the form

(5.2)

If we know v_n, we can calculate v_n+1. Another class of methods are the multistep methods.¹

Definition 5.1 A multistep method to approximate equation (5.1) is of the form

(5.3)

where α_j and β_j are given constants and r ≥ 1. The method is said to be explicit if β₋₁ = 0 and implicit otherwise.

The constants α_j and β_j, which ...