Introduction to Combinatorics, 2nd Edition

CHAPTER 5

ERROR-CORRECTING CODES

Sixteen unit hyperspheres can be arranged in R⁷ so that each hypersphere is tangent to exactly seven of the other hyperspheres.

This configuration of spheres is called a perfect packing. How do we obtain such a packing? What makes it perfect? What are its combinatorial properties? In this chapter and the next, we investigate such combinatorial designs, paying close attention to the interrelationships among the constructions and often finding equivalences between seemingly different structures. As a capstone, we construct the (23, 2¹², 7) Golay code G₂₃, the S(5, 8, 24) Steiner system, and Leech’s 24-dimensional lattice L. We begin our tour of combinatorial constructions with practical examples called codes.

5.1 Binary codes

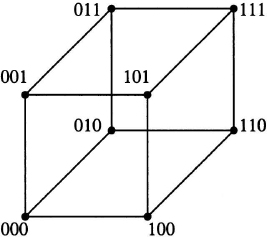
Let F = {0, 1}, the field of two elements. Then Fⁿ, the collection of strings of length n over F, is a vector space of dimension n over F. We can picture Fⁿ as the set of vertices of the n-dimensional unit hypercube. For example, Figure 5.1 depicts F³ as the set of vertices of the cube. These vertices are coordinatized with the eight vector representatives 000, 001, 010, 011, 100, 101, 110, and 111. Note that two vertices are edge adjacent if and only if their vector representatives differ in exactly one coordinate.

Figure 5.1 F³ as the set of vertices of a cube.

Given any two binary strings v, w Fⁿ, we define the Hamming distance ...