Introduction to Abstract Algebra, Solutions Manual, 4th Edition

Appendix B: Matrix Arithmetic

1. If A is invertible then B = IB = (A⁻¹A)B = A⁻¹0 = 0, contrary to assumption.

2. a. By the definition of matrix multiplication column k of AB is exactly AB_k .

3.AB = I₂ but .

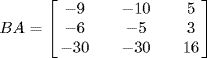
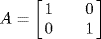
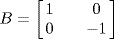
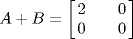
5. and are both invertible (in fact A⁻¹ = A and B⁻¹ = B), but is not invertible by Theorem 3 because det (A + B) = 0. For a simpler example, take A = U and B = − U for any invertible matrix U .

7.(A + B)(A − B) = A² + AB − BA − B², so (A − B)(A + B) = A² − B² if and only if AB − BA = 0.

9. It is routine that A³ = I, so AA² = I = A²A . This implies that A⁻¹ = A².

11. a. AA⁻¹ = I = A⁻¹A shows A is the inverse of A⁻¹, that is (A⁻¹)⁻¹ = A . Next, (AB)(B⁻¹A⁻¹) = AIA⁻¹ = AA⁻¹ = I, and similarly (B⁻¹A⁻¹)(AB) = I. Hence AB is invertible and (AB)⁻¹ = B⁻¹A⁻¹.

13. a.If AB = I then det A det B = det (AB) = det I = 1 . Hence det A is a unit so, by Theorem 7, A is invertible. But then A⁻¹ = A⁻¹I = A⁻¹(AB) = B, whence BA = A⁻¹A = I as required.

15. a. The only nonzero entry in E_ikE_mj must come from entry k of row i of E_ik and column m of E_mj . The result follows.

c. For each i and j, ...
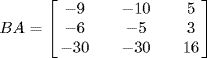