2
Correlation
Study the past if you would divine the future.
-Confucius
2.1 THE CORRELATION COEFFICIENT
2.1.1 Pearson’s Correlation
The correlation coefficient measures the strength and direction of correlation or corelation between two variables.
There are several methods, depending on the nature of data being studied, for calculating the correlation coefficient, but the best known is Pearson’s product-moment correlation coefficient, usually denoted by r, which is obtained by dividing the covariance of the two variables by the product of their standard deviations. The formula for calculating Pearson’s r is: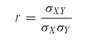
(2.1)
where σXY is the covariance of variables X and Y and σX, σy are their standard deviations. The covariance is the cross product of the deviations from the mean and is calculated by the following formula: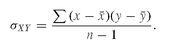
(2.2)
Unfortunately the size of the covariance depends on the values of measurement of each variable and is not normalized between −1.0 and +1.0 as is the correlation coefficient.
Substituting for the covariance in (1.1) we get: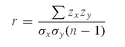 which is the average product of the z-scores, where and zy =
which is the average product of the z-scores, where and zy =
(2.3)
The correlation coefficient varies between – 1 and 1. A value of +1 indicates ...
Get Intermarket Trading Strategies now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

