Chapter 6
Dimensionless Equations: Similarity Parameters
6.1. Normalization of equations: Reynolds, Froude, and Prandtl numbers
We consider the following basic equations, written in tensorial form:
– continuity equation:
![]()
– equation of motion:
![]()
The last term of this equation represents the body forces acting within the fluid. In what follows, we consider this to be gravity whose expression is:
ρfi = ρgei
where g is the gravity acceleration and ei the unit vector indicating the direction of its action, generally the local vertical.
– energy equation:
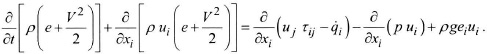
We assume that the gas is calorically perfect and the stress tensor τij can be written as:
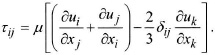
The purpose here is to give these equations dimensionless form by introducing non-dimensional quantities. This normalization operation is intended, in particular, to evaluate the relative importance of terms occurring in these equations that can lead to simpler forms if certain terms are very small, and therefore negligible, compared to other terms. Also, normalization will allow us to define similarity rules that enable us to transpose the obtained ...
Get Handbook of Compressible Aerodynamics now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

