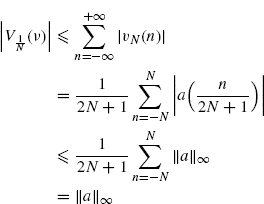3.9 Proofs for Section 2.6.1 “Discrete-Time Cyclic Cross-Correlogram”
3.9.1 Proof of Theorem 2.6.2 Expected Value of the Discrete-Time Cyclic Cross-Correlogram
By taking the expected value of both sides in (2.181) and using (2.174c) we get
(3.143) 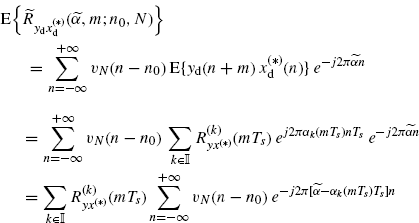
from which (2.183) immediately follows.
The data-tapering window ![]() is finite length (see (2.182)). Thus, in the first equality the sum over n is finite and can be freely interchanged with the expectation operator. In the second equality, Assumption 2.4.2a is used. In the third equality the order of the two sums can be interchanged since the double-index series over k and n is absolutely convergent (Johnsonbaugh and Pfaffenberger 2002, Theorem 29.4). In fact,
is finite length (see (2.182)). Thus, in the first equality the sum over n is finite and can be freely interchanged with the expectation operator. In the second equality, Assumption 2.4.2a is used. In the third equality the order of the two sums can be interchanged since the double-index series over k and n is absolutely convergent (Johnsonbaugh and Pfaffenberger 2002, Theorem 29.4). In fact,
(3.144) 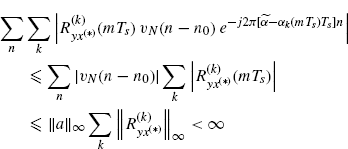
where Assumption 2.4.3a, (2.182), and the inequality (Assumption 2.4.5)
are used.
By substituting (2.182) into the first line of (2.184) we get
(3.146) 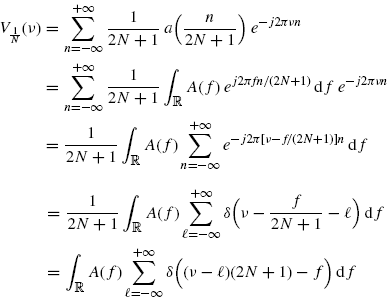
from which the right-hand side of (2.184) immediately follows. In (3.92), in the fourth equality the Poisson's sum formula ...
Get Generalizations of Cyclostationary Signal Processing: Spectral Analysis and Applications now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.