General theory of Relativity

2

Tensor Analysis and Riemannian Geometry

Part I Line Element

2.1 RIEMANNIAN SPACE

In the Euclidean space of three dimensions, each point is specified by three coordinates (x¹, x², x³). The distance ds between two neighbouring points (x¹, x², x³) and (x¹ + dx¹, x² + dx², x³ + dx³) is given by

 

ds² = (dx¹)² + (dx²)² + (dx³)²         (2.1)

 

We may extend the concept of Cartesian space in three dimensions to n-dimensional space. Each point will be designated by n coordinates (x¹,x²,…,xⁿ), which are shown collectively by (x). Further, we assume that the distance between any two neighbouring points is given by

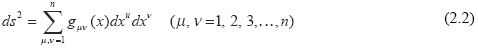
where g_μν (x) are functions of the coordinates ...