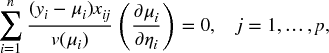CHAPTER 8 Quasi-Likelihood Methods
For a GLM ηi = g(μi) = ∑jβjxij, the likelihood equations
depend on the assumed probability distribution for yi only through μi and the variance function, v(μi) = var(yi). The choice of distribution for yi determines the relation v(μi) between the variance and the mean. Higher moments such as the skewness can affect properties of the model, such as how fast ![]() converges to normality, but they have no impact on the value of
converges to normality, but they have no impact on the value of ![]() and its large-sample covariance matrix.
and its large-sample covariance matrix.
An alternative approach, quasi-likelihood estimation, specifies a link function and linear predictor g(μi) = ∑jβjxij like a generalized linear model (GLM), but it does not assume a particular probability distribution for yi. This approach estimates {βj} by solving equations that resemble the likelihood equations (8.1) for GLMs, but it assumes only a mean–variance relation for the distribution of yi. The estimates are the solution of Equation (8.1) with v(μi) replaced by whatever variance function seems appropriate in a particular situation, with a corresponding adjustment for standard errors. To illustrate, a standard modeling approach for counts assumes that {yi} are independent Poisson ...
Get Foundations of Linear and Generalized Linear Models now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.