Flex and Bison are tools for building programs that handle structured input. They were originally tools for building compilers, but they have proven to be useful in many other areas. In this first chapter, we’ll start by looking at a little (but not too much) of the theory behind them, and then we’ll dive into some examples of their use.
The earliest compilers back in the 1950s used utterly ad hoc techniques to analyze the syntax of the source code of programs they were compiling. During the 1960s, the field got a lot of academic attention, and by the early 1970s, syntax analysis was a well-understood field.
One of the key insights was to break the job into two parts: lexical analysis (also called lexing or scanning) and syntax analysis (or parsing).
Roughly speaking, scanning divides the input into meaningful chunks, called tokens, and parsing figures out how the tokens relate to each other. For example, consider this snippet of C code:
alpha = beta + gamma ;
A scanner divides this into the tokens alpha, equal
sign, beta, plus sign, gamma, and semicolon. Then the parser determines that
beta + gamma is an expression, and
that the expression is assigned to alpha.
Scanners generally work by looking for patterns of characters in the input. For example, in a C program, an integer constant is a string of one or more digits, a variable name is a letter followed by zero or more letters or digits, and the various operators are single characters or pairs of characters. A straightforward way to describe these patterns is regular expressions, often shortened to regex or regexp. These are the same kind of patterns that the editors ed and vi and the search program egrep use to describe text to search for. A flex program basically consists of a list of regexps with instructions about what to do when the input matches any of them, known as actions. A flex-generated scanner reads through its input, matching the input against all of the regexps and doing the appropriate action on each match. Flex translates all of the regexps into an efficient internal form that lets it match the input against all the patterns simultaneously, so it’s just as fast for 100 patterns as for one.[1]
Unix systems (by which I also mean Unix-ish systems
including Linux and the BSDs) come with a word count program, which
reads through a file and reports the number of lines, words, and
characters in the file. Flex lets us write wc in a few dozen lines, shown in Example 1-1.
Example 1-1. Word count fb1-1.l
/* just like Unix wc */
%{
int chars = 0;
int words = 0;
int lines = 0;
%}
%%
[a-zA-Z]+ { words++; chars += strlen(yytext); }
\n { chars++; lines++; }
. { chars++; }
%%
main(int argc, char **argv)
{
yylex();
printf("%8d%8d%8d\n", lines, words, chars);
}Much of this program should look familiar to C programmers,
since most of it is C. A flex program consists of three sections,
separated by %% lines. The first
section contains declarations and option settings. The second section
is a list of patterns and actions, and the third section is C code
that is copied to the generated scanner, usually small routines
related to the code in the actions.
In the declaration section, code inside of %{ and %}
is copied through verbatim near the beginning of the generated C
source file. In this case it just sets up variables for lines, words,
and characters.
In the second section, each pattern is at the beginning of a
line, followed by the C code to execute when the pattern matches. The
C code can be one statement or possibly a multiline block in braces,
{ }. (Each pattern
must start at the beginning of the line, since
flex considers any line that starts with whitespace to be code to be
copied into the generated C program.)
In this program, there are only three patterns. The first one,
[a-zA-Z]+, matches a word. The
characters in brackets, known as a character
class, match any single upper- or lowercase letter, and the
+ sign means to match one or more
of the preceding thing, which here means a string of letters or a
word. The action code updates the number of words and characters seen.
In any flex action, the variable yytext is set to point to the input text
that the pattern just matched. In this case, all we care about is how
many characters it was so we can update the character count
appropriately.
The second pattern, \n, just
matches a new line. The action updates the number of lines and
characters.
The final pattern is a dot, which is regex-ese for any
character. (It’s similar to a ? in
shell scripts.) The action updates the number of characters. And
that’s all the patterns we need.[2]
The C code at the end is a main program that calls yylex(), the name that flex gives to the
scanner routine, and then prints the results. In the absence of any
other arrangements, the scanner reads from the standard input. So
let’s run it.
$ flex fb1-1.l $ cc lex.yy.c -lfl $ ./a.out The boy stood on the burning deck shelling peanuts by the peck ^D 2 12 63 $
First we tell flex to translate our program, and in classic Unix
fashion since there are no errors, it does so and says nothing. Then
we compile lex.yy.c, the C program
it generated; link it with the flex library, -lfl; run it; and type a little input for it
to count. Seems to work.
The actual wc program uses a
slightly different definition of a word, a string of non-whitespace
characters. Once we look up what all the whitespace characters are, we
need only replace the line that matches words with one that matches a
string of non-whitespace characters:
[^ \t\n\r\f\v]+ { words++; chars += strlen(yytext); }The ^ at the beginning of the
character class means to match any character other than the ones in
the class, and the + once again
means to match one or more of the preceding patterns. This
demonstrates one of flex’s strengths—it’s easy to make small changes
to patterns and let flex worry about how they might affect the
generated code.
Some applications are simple enough that you can write the whole thing in flex, or in flex with a little bit of C. For example, Example 1-2 shows the skeleton of a translator from English to American.
Example 1-2. English to American fb1-2.l
/* English -> American */
%%
"colour" { printf("color"); }
"flavour" { printf("flavor"); }
"clever" { printf("smart"); }
"smart" { printf("elegant"); }
"conservative" { printf("liberal"); }
… lots of other words …
. { printf("%s", yytext); }
%%It reads through its input, printing the American version when it matches an English word and passing everything else through. This example is somewhat unrealistic (smart can also mean hurt, after all), but flex is not a bad tool to use for doing modest text transformations and for programs that collect statistics on input. More often than not, though, you’ll want to use flex to generate a scanner that divides the input into tokens that are then used by other parts of your program.
The first program we’ll write using both flex and bison is a desk calculator. First we’ll write a scanner, and then we’ll write a parser and splice the two of them together.
To keep things simple, we’ll start by recognizing only integers, four basic arithmetic operators, and a unary absolute value operator (Example 1-3).
Example 1-3. A simple flex scanner fb1-3.l
/* recognize tokens for the calculator and print them out */
%%
"+" { printf("PLUS\n"); }
"-" { printf("MINUS\n"); }
"*" { printf("TIMES\n"); }
"/" { printf("DIVIDE\n"); }
"|" { printf("ABS\n"); }
[0-9]+ { printf("NUMBER %s\n", yytext); }
\n { printf("NEWLINE\n"); }
[ \t] { }
. { printf("Mystery character %s\n", yytext); }
%%The first five patterns are literal operators, written as quoted strings, and the actions, for now, just print a message saying what matched. The quotes tell flex to use the strings as is, rather than interpreting them as regular expressions.
The sixth pattern matches an integer. The bracketed pattern
[0-9]matches any single digit, and
the following + sign means to match
one or more of the preceding item, which here means a string of one or
more digits. The action prints out the string that’s matched, using
the pointer yytext that the scanner
sets after each match.
The seventh pattern matches a newline character, represented by
the usual C \n sequence.
The eighth pattern ignores whitespace. It matches any single
space or tab (\t), and the empty
action code does nothing.
The final pattern is the catchall to match anything the other patterns didn’t. Its action code prints a suitable complaint.
These nine patterns now provide rules to match anything that the user might enter. As we continue to develop the calculator, we’ll add more rules to match more tokens, but these will do to get us started.
In this simple flex program, there’s no C code in the third
section. The flex library (-lfl) provides a tiny main program
that just calls the scanner, which is adequate for this
example.
So let’s try out our scanner:
$ flex fb1-3.l $ cc lex.yy.c -lfl $ ./a.out 12+34 NUMBER 12 PLUS NUMBER 34 NEWLINE 5 6 / 7q NUMBER 5 NUMBER 6 DIVIDE NUMBER 7 Mystery character q NEWLINE ^D $
First we run flex, which translates the scanner into a C program
called lex.yy.c, then we compile
the C program, and finally we run it. The output shows that it
recognizes numbers as numbers, it recognizes operators as operators,
and the q in the last line of input
is caught by the catchall pattern at the end. (That ^D is a Unix/Linux end-of-file character. On
Windows you’d type ^Z.)
Most programs with flex scanners use the scanner to
return a stream of tokens that are handled by a parser. Each time the
program needs a token, it calls yylex(), which reads a little input and
returns the token. When it needs another token, it calls yylex() again. The scanner acts as a
coroutine; that is, each time it returns, it remembers where it was,
and on the next call it picks up where it left off.
Within the scanner, when the action code has a token ready, it
just returns it as the value from yylex(). The next time the program calls
yylex(), it resumes scanning with
the next input characters. Conversely, if a pattern doesn’t produce a
token for the calling program and doesn’t return, the scanner will
just keep going within the same call to yylex(), scanning the next input characters.
This incomplete snippet shows two patterns that return tokens, one for
the + operator and one for a
number, and a whitespace pattern that does nothing, thereby ignoring
what it matched.
"+" { return ADD; }
[0-9]+ { return NUMBER; }
[ \t] { /* ignore whitespace */ }This apparent casualness about whether action code returns often
confuses new flex users, but the rule is actually quite simple: If
action code returns, scanning resumes on the next call to yylex(); if it doesn’t return, scanning
resumes immediately.
Now we’ll modify our scanner so it returns tokens that a parser can use to implement a calculator.
When a flex scanner returns a stream of tokens, each
token actually has two parts, the token and the token’s
value. The token is a small integer. The token
numbers are arbitrary, except that token zero always means
end-of-file. When bison creates a parser, bison assigns the token
numbers automatically starting at 258 (this avoids collisions with
literal character tokens, discussed later) and creates a .h with definitions of the tokens numbers.
But for now, we’ll just define a few tokens by hand:
NUMBER = 258,
ADD = 259,
SUB = 260,
MUL = 261,
DIV = 262,
ABS = 263,
EOL = 264 end of line(Well, actually, it’s the list of token numbers that bison will create, as we’ll see a few pages ahead. But these token numbers are as good as any.)
A token’s value identifies which of a group of similar tokens
this one is. In our scanner, all numbers are NUMBER tokens, with the value saying what
number it is. When parsing more complex input with names,
floating-point numbers, string literals, and the like, the value says
which name, number, literal, or whatever, this token is. Our first
version of the calculator’s scanner, with a small main program for
debugging, is in Example 1-4.
Example 1-4. Calculator scanner fb1-4.l
/* recognize tokens for the calculator and print them out */
%{
enum yytokentype {
NUMBER = 258,
ADD = 259,
SUB = 260,
MUL = 261,
DIV = 262,
ABS = 263,
EOL = 264
};
int yylval;
%}
%%
"+" { return ADD; }
"-" { return SUB; }
"*" { return MUL; }
"/" { return DIV; }
"|" { return ABS; }
[0-9]+ { yylval = atoi(yytext); return NUMBER; }
\n { return EOL; }
[ \t] { /* ignore whitespace */ }
. { printf("Mystery character %c\n", *yytext); }
%%
main(int argc, char **argv)
{
int tok;
while(tok = yylex()) {
printf("%d", tok);
if(tok == NUMBER) printf(" = %d\n", yylval);
else printf("\n");
}
}We define the token numbers in a C enum. Then we make yylval, the variable that stores the token
value, an integer, which is adequate for the first version of our
calculator. (Later we’ll see that the value is usually defined as a
union so that different kinds of tokens can have different kinds of
values, e.g., a floating-point number or a pointer to a symbol’s entry
in a symbol table.)
The list of patterns is the same as in the previous example, but
the action code is different. For each of the tokens, the scanner
returns the appropriate code for the token; for numbers, it turns the
string of digits into an integer and stores it in yylval before returning. The pattern that
matches whitespace doesn’t return, so the scanner just continues to
look for what comes next.
For testing only, a small main program calls yylex(), prints out the token values, and,
for NUMBER tokens, also prints
yylval.
$ flex fb1-4.l $ cc lex.yy.c -lfl $ ./a.out a / 34 + |45 Mystery character a 262 258 = 34 259 263 258 = 45 264 ^D $
Now that we have a working scanner, we turn our attention to parsing.
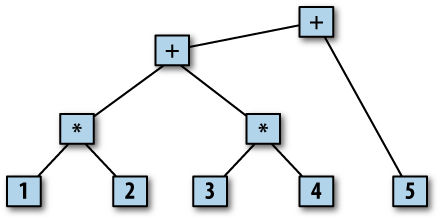
The parser’s job is to figure out the relationship among
the input tokens. A common way to display such relationships is a
parse tree. For example, under the usual rules of
arithmetic, the arithmetic expression 1 * 2 + 3
* 4 + 5 would have the parse tree in Figure 1-1.
Multiplication has higher precedence than addition, so the first
two expressions are 1 *
2 and 3 * 4. Then those two
expressions are added together, and that sum is then added to 5. Each
branch of the tree shows the relationship between the tokens or subtrees
below it. The structure of this particular tree is quite simple and
regular with two descendants under each node (that’s why we use a
calculator as the first example), but any bison parser makes a parse
tree as it parses its input. In some applications, it creates the tree
as a data structure in memory for later use. In others, the tree is just
implicit in the sequence of operations the parser does.
In order to write a parser, we need some way to describe the rules the parser uses to turn a sequence of tokens into a parse tree. The most common kind of language that computer parsers handle is a context-free grammar (CFG).[3] The standard form to write down a CFG is Backus-Naur Form (BNF), created around 1960 to describe Algol 60 and named after two members of the Algol 60 committee.
Fortunately, BNF is quite simple. Here’s BNF for simple
arithmetic expressions enough to handle 1 * 2
+ 3 * 4 + 5:
<exp> ::= <factor>
| <exp> + <factor>
<factor> ::= NUMBER
| <factor> * NUMBEREach line is a rule that says how to create
a branch of the parse tree. In BNF, ::= can be read “is a” or “becomes,” and
| is “or,” another way to create a
branch of the same kind. The name on the left side of a rule is a
symbol or term. By
convention, all tokens are considered to be symbols, but there are
also symbols that are not tokens.
Useful BNF is invariably quite recursive, with rules that refer to themselves directly or indirectly. These simple rules can match an arbitrarily complex sequence of additions and multiplications by applying them recursively.
Bison rules are basically BNF, with the punctuation simplified a little to make them easier to type. Example 1-5 shows the bison code, including the BNF, for the first version of our calculator.
Example 1-5. Simple calculator fb1-5.y
/* simplest version of calculator */
%{
#include <stdio.h>
%}
/* declare tokens */
%token NUMBER
%token ADD SUB MUL DIV ABS
%token EOL
%%
calclist: /* nothing */ matches at beginning of input
| calclist exp EOL { printf("= %d\n", $2); } EOL is end of an expression
;
exp: factor default $$ = $1
| exp ADD factor { $$ = $1 + $3; }
| exp SUB factor { $$ = $1 - $3; }
;
factor: term default $$ = $1
| factor MUL term { $$ = $1 * $3; }
| factor DIV term { $$ = $1 / $3; }
;
term: NUMBER default $$ = $1
| ABS term { $$ = $2 >= 0? $2 : - $2; }
;
%%
main(int argc, char **argv)
{
yyparse();
}
yyerror(char *s)
{
fprintf(stderr, "error: %s\n", s);
}Bison programs have (not by coincidence) the same three-part
structure as flex programs, with declarations, rules, and C code. The
declarations here include C code to be copied to the beginning of the
generated C parser, again enclosed in %{ and %}. Following that are %token token declarations, telling bison the
names of the symbols in the parser that are tokens. By convention,
tokens have uppercase names, although bison doesn’t require it. Any
symbols not declared as tokens have to appear on the left side of at
least one rule in the program. (If a symbol neither is a token nor
appears on the left side of a rule, it’s like an unreferenced variable
in a C program. It doesn’t hurt anything, but it probably means the
programmer made a mistake.)
The second section contains the rules in simplified BNF. Bison
uses a single colon rather than ::=, and since line boundaries are not
significant, a semicolon marks the end of a rule. Again, like flex,
the C action code goes in braces at the end of each rule.
Bison automatically does the parsing for you, remembering what rules have been matched, so the action code maintains the values associated with each symbol. Bison parsers also perform side effects such as creating data structures for later use or, as in this case, printing out results. The symbol on the left side of the first rule is the start symbol, the one that the entire input has to match. There can be, and usually are, other rules with the same start symbol on the left.
Each symbol in a bison rule has a value; the value of the target
symbol (the one to the left of the colon) is called $$ in the action code, and the values on the
right are numbered $1, $2, and so forth, up to the number of
symbols in the rule. The values of tokens are whatever was in yylval when the scanner returned the token;
the values of other symbols are set in rules in the parser. In this
parser, the values of the factor,
term, and exp symbols are the value of the expression
they represent.
In this parser, the first two rules, which define the symbol
calclist, implement a loop that
reads an expression terminated by a newline and prints its value. The
definition of calclist uses a
common two-rule recursive idiom to implement a sequence or list: the
first rule is empty and matches nothing; the second adds an item to
the list. The action in the second rule prints the value of the
exp in $2.
The rest of the rules implement the calculator. The rules with
operators such as exp ADD factor
and ABS term do the appropriate
arithmetic on the symbol values. The rules with a single symbol on the
right side are syntactic glue to put the grammar together; for
example, an exp is a factor. In the absence of an explicit action
on a rule, the parser assigns $1 to
$$. This is a hack, albeit a very
useful one, since most of the time it does the right thing.
Before we build the scanner and parser into a working
program, we have to make some small changes to the scanner in Example 1-4 so we can call it from the parser. In particular,
rather than defining explicit token values in the first part, we
include a header file that bison will create for us, which includes
both definitions of the token numbers and a definition of yylval. We also delete the testing main
routine in the third section of the scanner, since the parser will now
call the scanner. The first part of the scanner now looks like Example 1-6.
Example 1-6. Calculator scanner fb1-5.l
%{
# include "fb1-5.tab.h"
%}
%% same rules as before, and no code in the third sectionThe build process is now complex enough to be worth putting into
a Makefile:
# part of the makefile
fb1-5: fb1-5.l fb1-5.y
bison -d fb1-5.y
flex fb1-5.l
cc -o $@ fb1-5.tab.c lex.yy.c -lflFirst it runs bison with the -d (for “definitions” file) flag, which
creates fb1-5.tab.c and fb1-5.tab.h, and it runs flex to create
lex.yy.c. Then it compiles them
together, along with the flex library. Try it out, and in particular
verify that it handles operator precedence correctly, doing
multiplication and division before addition and subtraction:
$ ./fb1-5 2 + 3 * 4 = 14 2 * 3 + 4 = 10 20 / 4 - 2 = 3 20 - 4 / 2 = 18
The reader may be wondering at this point whether the grammar in Example 1-5 is needlessly complicated. Why not just write this?
exp: exp ADD exp | exp SUB exp | exp MUL exp | exp DIV exp | ABS exp | NUMBER ;
There are two answers: precedence and ambiguity. The separate symbols for term, factor, and exp tell bison to handle ABS, then MUL and DIV, and then ADD and SUB. In general, whenever a grammar has
multiple levels of precedence where one kind of operator binds “tighter”
than another, the parser will need a level of rule for each
level.
Well, then, OK, how about this?
exp: exp ADD exp
| exp SUB exp
| factor
;
similarly for factor and termOne of bison’s greatest strengths, and simultaneously one
of its most annoying aspects, is that it will not parse an
ambiguous grammar. That is, any parser that bison creates has
exactly one way to parse any input that it parses, and the parser will
accept exactly that grammar. The previous grammar is ambiguous, because
input such as 1 - 2 + 3 could be
parsed either as (1-2) + 3 or as
1 - (2+3), two different expressions
with different values. Although there are some cases where ambiguity
doesn’t matter (e.g., 1+2+3), in most
cases the ambiguity really is an error, and the grammar needs to be
fixed. The way we wrote the grammar in Example 1-5 makes
expressions unambiguously group to the left. If a grammar is ambiguous,
bison reports conflicts, places where there are two
different possible parses for a given bit of input. It creates a parser
anyway, picking one option in each conflict, but that choice means the
language it’s parsing isn’t necessarily the one you tried to specify. We
discuss this at length in Chapter 7.
Bison’s usual parsing algorithm can look ahead one token to decide what rules match the input. Some grammars aren’t ambiguous but have places that require more than one token of lookahead to decide what rules will match. These also cause conflicts, although it is usually possible to rewrite the grammar so that one token lookahead is enough.
Actually, the previous discussion about ambiguity is not quite
true. Since expression grammars are so common and useful, and since
writing separate rules for each precedence level is tedious, bison has
some special features that let you write an expression grammar in the
natural way with one rule per operator in the form exp OP exp and just tell it what precedence
and grouping rules to use to resolve the ambiguity. We’ll learn about
these in Chapter 3. Also, bison has an alternative
parsing technique called GLR that can handle ambiguous grammars and
arbitrary lookahead, tracking all the possible parses that match the
input in parallel. We cover this in Chapter 9.
One of the nicest things about using flex and bison to
handle a program’s input is that it’s often quite easy to make small
changes to the grammar. Our expression language would be a lot more
useful if it could handle parenthesized expressions, and it would be
nice if it could handle comments, using // syntax. To do this, we need only add one
rule to the parser and three to the scanner.
In the parser we define two new tokens, OP and CP
for open and close parentheses, and add a rule to make a parenthesized
expression a term:
%token OP CP in the declaration section ... %% term: NUMBER | ABS term { $$ = $2 >= 0? $2 : - $2; } | OP exp CP { $$ = $2; } New rule ;
Note the action code in the new rule assigns $2, the value of the expression in the
parentheses, to $$.
The scanner has two new rules to recognize the two new tokens and
one new rule to ignore two slashes followed by arbitrary text. Since a
dot matches anything except a newline, .* will gobble up the rest of the line.
"(" { return OP; }
")" { return CP; }
"//".* /* ignore comments */That’s it—rebuild the calculator, and now it handles parenthesized expressions and comments.
The two example programs in this chapter, word count and a calculator, are both simple enough that we could without too much trouble have written them directly in C. But there is little reason to do so when developing a program. The pattern-matching technique that flex uses is quite fast and is usually about the same speed as a handwritten scanner. For more complex scanners with many patterns, a flex scanner may even be faster, since handwritten code will usually do many comparisons per character, while flex always does one. The flex version of a scanner is invariably much shorter than the equivalent C, which makes it a lot easier to debug. In general, if the rules for breaking an input stream into tokens can be described by regular expressions, flex is the tool of choice.
Similarly, a bison parser is much shorter and easier to debug than the equivalent handwritten parser, particularly because of bison’s verification that the grammar is unambiguous.
Will the calculator accept a line that contains only a comment? Why not? Would it be easier to fix this in the scanner or in the parser?
Make the calculator into a hex calculator that accepts both hex and decimal numbers. In the scanner add a pattern such as
0x[a-f0-9]+to match a hex number, and in the action code usestrtolto convert the string to a number that you store inyylval; then return aNUMBERtoken. Adjust the outputprintfto print the result in both decimal and hex.(extra credit) Add bit operators such as
ANDandORto the calculator. The obvious operator to use forORis a vertical bar, but that’s already the unary absolute value operator. What happens if you also use it as a binaryORoperator, for example,exp ABS factor?Does the handwritten version of the scanner from Example 1-4 recognize exactly the same tokens as the flex version?
Can you think of languages for which flex wouldn’t be a good tool to write a scanner?
Rewrite the word count program in C. Run some large files through both versions. Is the C version noticeably faster? How much harder was it to debug?
[1] The internal form is known as a deterministic finite automation (DFA). Fortunately, the only thing you really need to know about DFAs at this point is that they’re fast, and the speed is independent of the number or complexity of the patterns.
[2] The observant reader may ask, if a dot matches anything, won’t it also match the letters the first pattern is supposed to match? It does, but flex breaks a tie by preferring longer matches, and if two patterns match the same thing, it prefers the pattern that appears first in the flex program. This is an utter hack, but a very useful one we’ll see frequently.
[3] CFGs are also known as phrase-structure grammars or type-2 languages. Computer theorists and natural-language linguists independently developed them at about the same time in the late 1950s. If you’re a computer scientist, you usually call them CFGs, and if you’re a linguist, you usually call them PSGs or type-2, but they’re the same thing.
Get flex & bison now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.