Chapter 35
Generalized Catalan Numbers
We know that for n ≥ 0, the nth Catalan number is given by
![]()
which can be rewritten as
![]()
But why would we want to do this?
If we let k denote a fixed positive integer, then we can define the generalized Catalan number Ck(n) as
![]()
When k = 2 we find that C2(n) = Cn, our familiar nth Catalan number. For k = 1 we have C1(n) = nn = 1, for n ≥ 0.
Corresponding to the cases for k = 3 and k = 4, we find the sequences
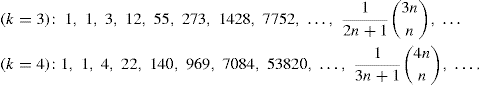
Based on what we have seen so far, it seems that these generalized Catalan numbers are all integers. This is indeed the case, as we shall now establish. Before doing so, however, we need to recall the following facts about the 291 system of integers:
1. If a and b are positive integers, then the greatest common divisor of a and b, denoted gcd (a, b), is the smallest positive integer that can be written as a linear combination of a and b—so there exist integers s and t with gcd (a, b) = as + bt and no smaller positive integer can be expressed in this manner.
2. If a and b are positive integers with gcd (a, b) = 1, then we say that a and b are ...

