Chapter 7
Tilings: Divisibility Properties of the Fibonacci Numbers
Further properties of the Fibonacci numbers arise as we examine problems that deal with various ways to tile certain types of chessboards.
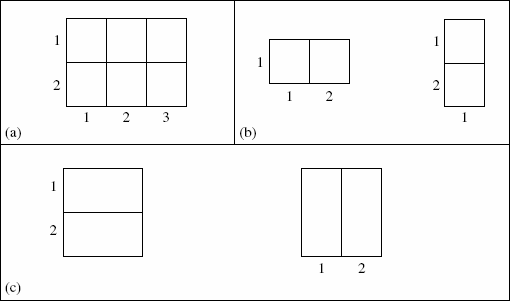
Example 7.1: Let us start with a 2 × n chessboard, where n ≥ 1. The case for n = 3 is shown in Fig. 7.1 (a). We want to cover such a chessboard using 1 × 2 (horizontal) dominoes, which we can also use as 2 × 1 (vertical) dominoes. Such dominoes (or tiles) are shown in Fig. 7.1 (b).
For n ≥ 1, let qn count the number of ways we can cover (or tile) a 2 × n chessboard using the 1 × 2 and 2 × 1 dominoes. Here q1 = 1, since a 2 × 1 chessboard requires one 2 × 1 (vertical) domino. A 2 × 2 chessboard can be covered in two ways—using two 1 × 2 (horizontal) dominoes or two 2 × 1 (vertical) dominoes, as demonstrated in Fig. 7.1 (c). So q2 = 2. For n ≥ 3, we consider the last (nth) column of a 2 × n chessboard. This column can be covered in two ways;
(i) By one 2 × 1 (vertical) domino: Then the remaining 2 × (n − 1) chessboard can be covered in qn−1 ways.
(ii) By the right squares of two 1 × 2 (horizontal) dominoes placed one on top of the other: Here the remaining 2 × (n − 2) chessboard can be covered in qn−2 ways.
The two ways mentioned in (i) and (ii) cover all the possibilities and have nothing in common, so we arrive at
and
Example 7.2: Now we shall start with a 1 ...