Chapter 5
Some Introductory Examples
As the title indicates, this chapter will provide some examples where the Fibonacci numbers arise. In particular, one such example will show us how to write a Fibonacci number as a sum of binomial coefficients. In addition, even more examples will arise from some of the exercises for the chapter.
Example 5.1: Irving Kaplansky (1917-2006): For n ≥ 1, let Sn = {1, 2, 3, . . ., n}, and let S0 = ∅, the null, or empty, set. Then the number of subsets of Sn is 2n. But now let us count the number of subsets of Sn with no consecutive integers. So, for n ≥ 0, we shall let an count the number of subsets of Sn that contain no consecutive integers. We consider the situation for n = 3, 4, and 5. In each case, we find the empty set ∅; otherwise, there would have to exist two integers in ∅ of the form x and x + 1. Either such integer contradicts the definition of the null set. So the subsets with no consecutive integers for these three cases are as follows:
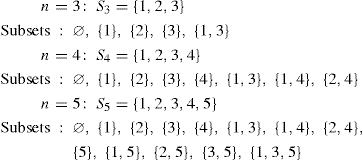
Note that when we consider the case for n = 5, only two situations can occur, and they cannot occur simultaneously:
i. 5 is not in the subset: Here we can use any of the eight subsets for S4—as we see from the first line of subsets for S5.
ii. 5 is in the subset: Then we cannot have 4 in the subset. So we place the integer 5 in each of the five subsets for S3 and arrive at the five subsets in the second ...

