Examples and Problems in Mathematical Statistics

PART III: PROBLEMS

Section 2.2

2.2.1 Consider the binomial distribution with parameters n, θ, 0 < θ < 1.

Write an algorithm for the computation of b(j | n, θ) employing the recursive relationship

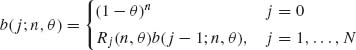
where Rj (n, θ) = b(j;n, θ)/b(j – 1; n, θ). Write the ratio Rj (n, θ) explicitly and find an expression for the mode of the distribution, i.e., = smallest nonnegative integer for which b(x0;n, θ) ≥ b(j; n, θ) for all j = 0, …, n.

2.2.2 Prove formula (2.2.2).

2.2.3 Determine the median of the binomial distribution with n = 15 and θ = .75.

2.2.4 Prove that when n → ∞, θ → 0, but nθ → λ, 0 < λ < ∞, then

where p(i; λ) is the p.d.f. of the Poisson distribution.

2.2.5 Establish formula (2.2.7).

2.2.6 Let X have the Pascal distribution with parameters ν (fixed positive integer) and θ, 0 < θ < 1. Employ the relationship between the Pascal distribution and the negative–binomial distribution to show that the median of X is ν + n.5, where n.5 = least nonnegative integer n such that Iθ (ν, n + 1) ≥ .5. [This formula of the median is useful for writing a computer program and utilizing the computer’s library subroutine function that computes Iθ (a, b).]

2.2.7 Apply formula (2.2.4) to prove the binomial ...