Chapter 1. Functions and Variables
This chapter starts with a couple of âwarm-up exercisesâ so that you can get comfortable with your ClojureScript development environment. First, a quick review of how to define functions. Here is the generic model for a function:
(defn function-name [parameters] function-body)
Here is a function that takes an acceleration and an amount of time as its parameters and returns the distance traveled:
(defn distance [accel time] (/ (* accel time time) 2.0)
You can also put a documentation string between the function name and parameter list:
(defn distance "Calculate distance traveled by an object moving with a given acceleration for a given amount of time." [accel time] (/ (* accel time time) 2.0)
Ãtude 1-1: Defining a Function in the REPL
Create a project named formulas (see âCreating a ClojureScript Projectâ) and start a browser REPL (read/evaluate/print/loop). If you havenât yet installed ClojureScript, follow the instructions in Appendix B, and create a project to work with.
In the REPL, type the preceding distance function and test it.
Ãtude 1-2: Defining Functions in a Source File
Defining functions in the REPL is fine for a quick test, but it is not something you want to do on an application-level scale. Instead, you want to define the functions in a source file. In the formulas project, open the src/formulas/core.cljs file and create functions for these formulas:
- Distance equals one-half acceleration multplied by time squared:
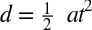
- Kinetic energy equals one-half the mass times velocity squared:
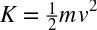
- Centripetal acceleration is velocity squared over the radius:
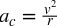
Here is some sample output. (in-ns 'formulas.core) switches you to that namespace so that you can type the function name without having to specify the module that it is in. If you update the source, (require 'formulas.core :reload) will recompile the code:
cljs.user=> (in-ns 'formulas.core) nil formulas.core=> (require 'formulas.core :reload) nil formulas.core=> (distance 9.8 5) 122.5 formulas.core=> (kinetic-energy 35 4) 280 formulas.core=> (centripetal 30 2) 450
See a suggested solution: âSolution 1-2â.
Ãtude 1-3: Using def
The def special form lets you bind a symbol to a value. The symbol is globally available to all functions in the namespace where it is defined. Add a function named gravitational-force that calculates the gravitational force between two masses whose centers of mass are at a distance r from each other to your code:
, where the gravitational constant
Use a def for the gravitational constant.
Here is the calculation for two masses of 100 kg that are 5 m apart:
formulas.core=> (gravitational-force 100 100 5) 2.67136e-8
Redefining and def
ClojureScriptâs def creates an ordinary JavaScript variable. Note that it is possible
to rebind a symbol to a value with code like this:
(defx5)(defx6)(defx(+1x))
However, this is somewhat frowned upon. Global, shared, mutable (changeable) variables can be problematic, as described in this answer to a question on StackExchange. You will find that ClojureScriptâs functional programming model makes the need for such global variables much less frequent. As a beginning programmer, when you create a variable with def, treat it as if it were an (unalterable) algebraic variable and do not change its value.
See a suggested solution: âSolution 1-3â
Ãtude 1-4: Using let
To create local bindings of symbols to values within a function, you use let. The let is followed by a vector of symbol and value pairs.1
In this étude, you will write a function named monthly-payment that calculates monthly payments on a loan. Your function will take the amount of the loan, the annual percentage rate, and the number of years of the loan as its three parameters. Calculate the monthly payment according to this formula:
- p is the principal (the amount of the loan).
- r is the monthly interest rate.
- n is the number of months of the loan.
Use let to make local bindings for:
- The monthly interest rate r, which equals the annual rate divided by 12
- The number of months n, which equals the number of years times 12
- The common subformula
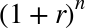
To raise a number to a power, invoke the JavaScript pow function with code in this format:
(.powjs/Mathnumberpower);; Thus, to calculate 3 to the fifth power:(.powjs/Math35)
You can also use this shorthand:
(js/Math.pow35)
You will learn more about interacting with JavaScript in Chapter 2.
Here is some sample output for a loan of $1,000.00 at 5.5% for 15 years. You can also check the results of your function against the results of the PMT function in your favorite spreadsheet:
formulas.core=>(monthly-payment10005.515)8.17083454621138
See a suggested solution: âSolution 1-4â.
Ãtude 1-5: More Practice with def and let
Hereâs a somewhat more complicated formulaâdetermining the amount of sunlight in a day, given the day of year and the latitude of your location.
Write a function named daylight with two parameters: a latitude in degrees and a Julian day. The function returns the number of minutes of
sunshine for the day, using the formula explained at the Ask Dr. Math website. The latitude is in degrees, but JavaScriptâs trigonometric functions use radians, so you will need a function to convert degrees to radians, and Iâll give you that for free:
(defnradians"Convert degrees to radians"[degrees](*(/(.-PIjs/Math)180)degrees))
The expression (.-PIÂ js/Math) gets the PI property of the JavaScript Math object.
- You will want a variable that holds the latitude converted to radians.
- Calculate
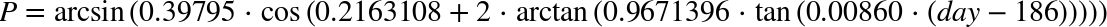
- Calculate
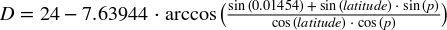
The variable D holds the number of hours of daylight, so multiply that by 60 for your final result. If you feel that these formulas are a bit too complicated to type as single expressions (I certainly did!), break them down by using let for the parts.
On Mac OSX or Linux, you can get a Julian date with the date command:
$ date '+%j' # today 127 $ date -d '2015-09-15' '+%j' # arbitrary date 258
Your results should be very close to those generated by the National Oceanic and Atmospheric Administration spreadsheets, which use a far more complicated algorithm than the one given here.
See a suggested solution: âSolution 1-5â.
1 Technically, let is followed by a vector of binding forms and values. Binding forms include destructuring as well as simple symbols.
Get Etudes for ClojureScript now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

