CHAPTER 10
American Monte Carlo
10.1 INTRODUCTION
Traditionally, the numerical techniques for pricing derivatives fall into two distinct categories: Monte Carlo simulation and backwards induction methods such as trees or PDE methods. The following table sums up the strengths of each type:

In the most general terms, a derivative consists of a series of payments that depend on decisions made by the two parties in the contract and the values of some quantities observable in the market: the underlyings, which we will model with some stochastic processes. The payments can depend on the values of the underlyings observed on the date of the payment or on some functional of the paths followed by the underlyings up to the payment date.
To price derivatives using PDE methods, we must be able to represent the price of the derivative at time t as a function of a small number of state variables. For path-dependent options, the number of state variables may be larger than the number of underlyings. For instance, were we pricing an Asian option, our state-space at time t would have to include the current stock price and the running average stock price.
If we assume that our stock price follows the Black-Scholes SDE, and that the average is defined as
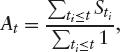
for some set of averaging dates ti, then we ...
Get Equity Hybrid Derivatives now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

