Electrothermics

1.5. Solving the electromagnetic and thermal equations

The electromagnetic and thermal equations are partial differential equations, where the unknown is either a scalar or a vector quantity dependent on spatial coordinates and time. Numerical methods are often used to solve these equations. Nevertheless, in certain simple cases and for the comprehension of the involved physical phenomena, analytic methods are interesting.

1.5.1. Analytic methods

1.5.1.1. Transient state

In the one-dimensional case, the general form of the electromagnetic and thermal equations is as follows:

[1.58]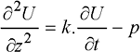

where, z is the propagation direction of the wave U and, p, represents internal sources.

For example, the one-dimensional formulation of magnetic potential A is:

[1.59]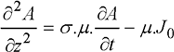

and for the formulation in H, we obtain:

[1.60]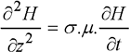

As for the thermal equation, it can be written as:

[1.61]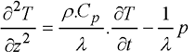

1.5.1.2. Harmonic state

For a sinusoidal variation, the general form is given by:

[1.62]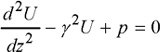

where with as the penetration depth of wave ...