Answers to Some Problems
P1.2 a) e′1 = cos φ e1 + sin φ e2, e′2 = −sin φ e1 + cos φ e2, e′3 = e3
A′1 = A1 cos φ + A2 sin φ, A′2 = − A1 sin φ + A2 cos φ, A′3 = A3
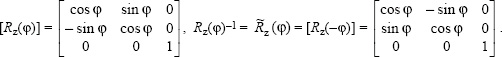
b) B = (μoI/2πr′2)(−y′ e′x + x′ e′y) is a vector equal to (μoI2πr′2)( e′z × r′), while B′ = (μoI/2πr′2) [(x′ sin 2φ + y′ cos 2φ) e′1 + (x′ cos 2φ − y′ sin 2φ) e′2] is not a vector.
P1.4 ![]() n.E(r) = 4πR2f(R), ∇.E = 2f/r + ∂rf and
n.E(r) = 4πR2f(R), ∇.E = 2f/r + ∂rf and ![]() ∇.E = 4πR2f(R).
∇.E = 4πR2f(R).
P1.5 Let x′α = Σβ Rβα xβ. We find ∂α = Σβ ∂′β.(∂x′ β/∂xα) = Σβ ∂′β Rαβ = Σβ Rαβ ∂′β.
P1.6 b) If dr is on V = Constant, dV = Σα ∂αV dxα = ∇ V.dr = 0, hence ∇V is normal to dr. c) If only x varies, as r2 = x2 + y2 + z2, we get 2r dr = 2x dx, hence ∂αr = xα/r and ∂αf(r) = (df/dr)(∂αr) = (df/dr)(xα/r). If f = K/r, we find ∂αf(r) = (−K/r2)(xα/r) = −Kxα/r3.
P1.8 a) If V = K(p.r)/r3, E = −∇V = (K/r3)[3(p.r) r/r2 − p]. If p = pez, V = Kpz/r3 and E = (Kp/r3)[3zr/r2 −ez]. b) If ![]() , we find
, we find ![]() .Using spherical coordinates, if , we find sin θ eφ/r2 and
.
.Using spherical coordinates, if , we find sin θ eφ/r2 and
.
P1.9 As ∇ × E = 0, E is the gradient of ...
Get Electromagnetism: Maxwell Equations, Wave Propagation and Emission now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

