7.2. Approach to estimation
7.2.1. Scalar case
It is clear that we can give an estimate of the magnitude of a process based on past observation of this process.
In the expression of the innovation:
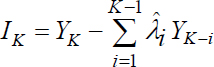
YK represents the magnitude to be estimated (see predictor) and 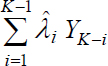 represents the estimation.
represents the estimation.
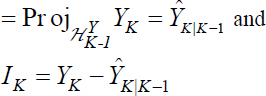
In the same way, if we call:
![]()
the estimate of a process at instant K, starting from measurement y1, …, yK, … of process Y1, …, YK, …, we can write:
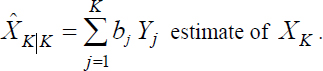
Let us write the innovation at instants 1, 2,…, K :
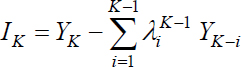
with ![]() : coefficients of the predictor of order K − 1
: coefficients of the predictor of order K − 1
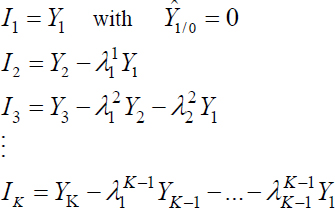
This expression can be put in the form: I = M Y
with M, invertible triangular matrix because |det M| = 1.
Thus Y = M−1 I.
As a consequence, each vector I
Get Discrete Stochastic Processes and Optimal Filtering now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

