Discrete Stochastic Processes and Optimal Filtering

4.2. Linear estimation

The fundamental space that we define below has already been introduced in Chapter 3 but in a different context.

DEFINITION.– Space up to instant K − 1 is called linear space of observation and the vector space of the linear combinations of r.v. 1, Y₁, …, Y_k−1 is denoted (or ), i.e.:

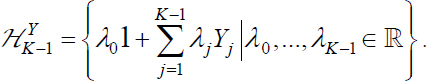
Since r.v. 1, Y₁, …, Y_k−1 ∈ L²(dP) , is a vector subspace (closed, as the number of r.v. is finite) of L²(dP).

We can also say that is a Hilbert subspace of L² (dP).

We are focusing here on the problem stated in the preceding section but with a simplified hypothesis: g is linear, which means that the envisaged estimators Z of X_K are of the form:

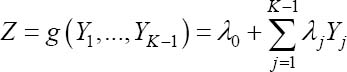and thus belong to .

The problem presents itself as: find the r.v., denoted , which renders minimum mapping:

(i.e., find which render minimum: ...