Discrete Stochastic Processes and Optimal Filtering

2.6. Exercises for Chapter 2

Exercise 2.1.

We are looking at a circular target D of center 0 and of radius R which is used for archery. The couple Z = (X, Y) represents the coordinates of the point of impact of the arrow on the target support; we assume that the r.v. X and Y are independent and following the same law N (0.4R²).

1) What is the probability that the arrow reach the target?

2) How many times must one fire the arrow In order for, with a probability ≥ 0.9, the target is reached at least once (we give n 10 ≠ 2.305).

Let us assume that we fire 100 times at the target, calculate the probability that the target to reached at least 20 times.

Hint: use the central limit theorem.

Solution 2.1.

1) The r.v.s X and Y being independent, the density of probability of Z = (X, Y) is f_Z (x, y) = f_X (x) f_Y (y) = 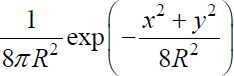and P (Z ∈ D) = 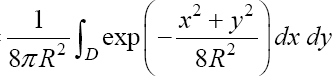using a change from Cartesian to polar coordinates:

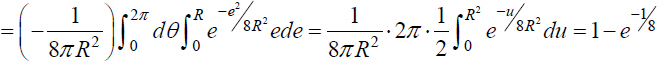
2) At each shot k, we associate a Bernoulli r.v. U_k ∼ b (p) defined by

In n shots, the number of impacts is given ...