Examples treated using Matlab software
First example of Kalman filtering
The objective is to estimate an unknown constant drowned in noise.
This constant is measured using a noise sensor.
The noise is centered, Gaussian and of variance equal to 1.
The initial conditions are equal to 0 for the estimate and equal to 1 for the variance of the estimation error.
clear t=0:500; R0=1; constant=rand(1); n1=randn(size(t)); y=constant+n1; subplot(2,2,1) %plot(t,y(1,:)); plot(t,y,’k’);% in B&W grid title(‘sensor’) xlabel(‘time’) axis([0 500 -max(y(1,:)) max(y(1,:))]) R=R0*std(n1)^2;% variance of noise measurement P(1)=1;%initial conditions on variance of error estimation x(1)=0; for i=2:length(t) K=P(i-1)*inv(P(i-1)+R); x(i)=x(i-1)+K*(y(:,i)-x(i-1)); P(i)=P(i-1)-K*P(i-1); end err=constant-x; subplot(2,2,2) plot(t,err,’k’); grid title(‘error’); xlabel(‘time’) axis([0 500 -max(err) max(err)]) subplot(2,2,3) plot(t,x,’k’,t,constant,’k’);% in W&B title(‘x estimated’) xlabel(‘time’) axis([0 500 0 max(x)]) grid subplot(2,2,4) plot(t,P,’k’);% in W&B grid,axis([0 100 0 max(P)]) title(‘variance error estimation’) xlabel(‘time’)
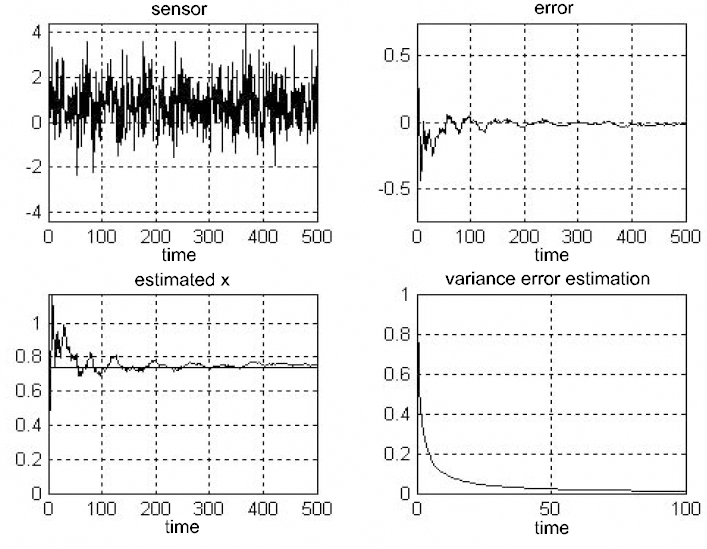
Figure 7.3. Line graph of measurement, error, best filtration and variance of error
Second example of Kalman filtering
The objective of this example is to extract a dampened sine curve of the noise.
The state vector is a two component column vector:
The system noise is centered, ...
Get Discrete Stochastic Processes and Optimal Filtering now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

