Direct Eigen Control for Induction Machines and Synchronous Motors

Appendix C

Transfer Matrix Inversion

To invert one matrix P, the various steps are as follows:

• calculate its determinant det(P)
• calculate the cofactor p_ij of each element, starting from the determinant of the corresponding minor matrix P_{ij} of P, i.e. the matrix P, in which one removes the row i and the column j:

(C.1)    

• constitute the cofactor matrix, or the matrix of the cofactors:

(C.2)    

• calculate the transpose cofactor matrix com(P)T, adjugate of P
• calculate the inverse of P by:

(C.3)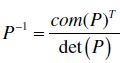    

These algebraic calculations are heavy, rather than complex. We will, however, carry them out for the IPM-SM, for inverting the transfer matrix P (equation (B.37)); this result is indeed necessary to calculate the control vector.

The following calculations will not detail the intermediate calculation of the coefficients cij of the adjugate of the P matrix, since it is enough to:

• calculate the 3 × 3 determinants of the minor matrices of P, using Cramer’s rules
• give to the determinants, the corresponding sign (−1)^{i + j}
• invert the subscripts i and j to create the coefficients cp_ij, of the adjugate matrix:

(C.4)    

To calculate the inverse matrix P^{− 1}, we will thus calculate firstly the determinant of the transfer ...