4.3. Exercises
EXERCISE 4.4.
Suppose that the probability of measuring k points of a random process X within an interval T, is Pk = c ak, for k ≥ 0.
1. Determine the value of the constant c as a function of parameter a, which belongs to an interval to be specified.
2. Demonstrate that E[K] = a/(1-a).
3. Calculate the probability of having at least k points within the interval T.
4. The following results are issued from process observations:

- Give an estimation of a.
- Verify if the measured values obey the distribution defined above.
- Explain why these values are trustworthy or not.
EXERCISE 4.5.
In order to control the homogenity of a factory production, 1,000 samples of a manufactured mechanical part are randomly selected. The size X measured for each of them is recorded in the table below:
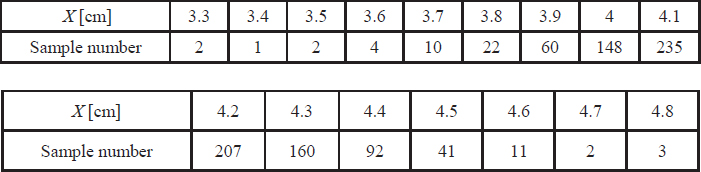
The problem is to know if the distribution of X can be considered as Gaussian.
1. Calculate the empirical mean value, variance and standard deviation.
2. Plot the histogram and conclude.
3. For a Gaussian variable, what is the probability of having a value up to 2σ from its mean value?
4. Give a probability for 4 ≤ X ≤ 4.2 and conclude.
5. Validate your conclusion using one or two statistical tests.
EXERCISE 4.6.
The following values are recorded with a receiver:
1. Sort these values in increasing ...
Get Digital Signal Processing Using Matlab now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

