4.2. Solved exercises
EXERCISE 4.1.
Consider 2,048 samples of a Gaussian white random process P with a unit mean value and a variance of 0.25. Check if it is a Gaussian random variable using different tests.
% Random process generation P=0.5*randn(1,2048)+1; mp = mean(P) vp = var(P)
1st test: the simplest test uses the random process histogram.
bins = 20; hist(P,bins);
It can easily be seen that the obtained histogram is very similar to a Gaussian pdf.
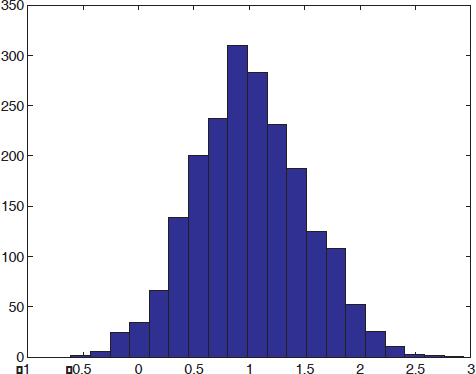
Figure 4.2. Histogram of a Gaussian random process
2nd test: Let us calculate 3rd and 4th order cumulants of the random process P using equations [4.6] and [4.7].
Cum3 = mean(P.^3) - 3*mean(P)*mean(P.^2)+2* mean(P)^3 Cum4 = mean(P.^4) - 4*mean(P)*mean(P.^3) - 3*mean(P.^2)^2 + 12*mean(P)^2*mean(P.^2)- 6*mean(P)^4 Cum3 = 0.0234 Cum4 = 0.0080
The obtained values for the two cumulants are close to zero, so the Gaussianity hypothesis on P is reinforced.
3rd test: Henry line.
nb_bins = 20;
[hv,x]=hist(P,nb_bins);
F=cumsum(hv)/sum(hv); F(end)=0.999 ;% empirical cdf
y=norminv(F,0,1); % percentile of a N(0,1) distributed variable
% Graphical matching
p=polyfit(x,y,1); % linear matching of x and y
s=1/p(1) % standard deviation estimation = inverse of the slope
z=polyval(p,x); % values on the Henry line
figure;
hold on;
plot(x,z,'-r');
plot (x,y,'*');
legend.('Henry line', 'Couples (x,t)');
xlabel('x');
ylabel('t');
Figure 4.3. Henry ...
Get Digital Signal Processing Using Matlab now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

