2.2. Solved exercises
EXERCISE 2.1.
The MATLAB code below generates and plots some basic discrete-time signals.
subplot (3,3,1);
stem([1;zeros (49,1)]);
title('Dirac pulse')
subplot(3,3,2); stem(ones(50,1));
title(' Step function')
subplot (3,3,3);
stem ([ones (1,5),zeros(1,3)])
title(' Rectangular pulse')
subplot (3,3,4);
stem(sin(2*pi/8*(0:15)) )
title('Sinusoidal signal')
subplot (3,3,5); stem(sinc(0:0.25:8)) ;
title('“Sinc” signal')
subplot (3,3,6); stem(exp(- (0:15)));
title('e^-^n signal')
subplot (3,3,7);
stem(pow2(-0.5*(0:15)))
title('2^-^0^.^5^n signal')
subplot(3,3,8); stem(3.^(0:15));
title('3^n signal')
subplot(3,3,9); stem (randn(1,16));
title('Gaussian random signal')
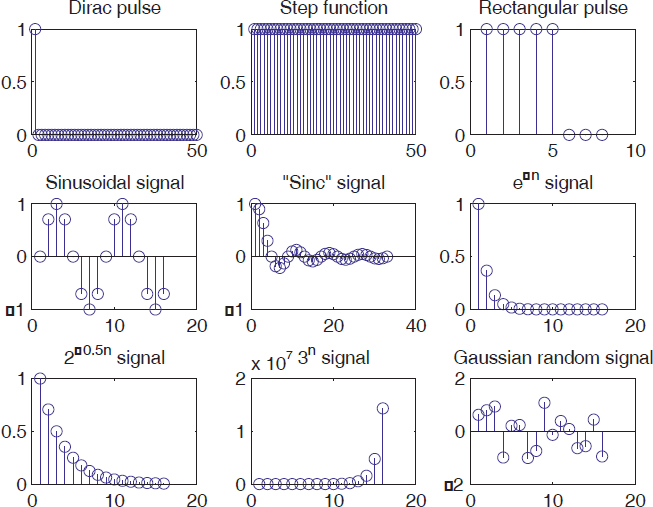
Figure 2.1. Examples of discrete-time signals
EXERCISE 2.2.
Generate the following signal:
x(n) = K · exp[c · n],
where: K = 2, c = −1/12 + jπ/6, n ![]() N and n = 0..40 .
N and n = 0..40 .
c = -(1/12) + (pi/6)*i;
K = 2; n = 0:40;
x = K*exp(c*n);
subplot (2,1,1); stem(n, real(x));
xlabel('Iime index n');
ylabel('Amplitude');
title('Real part');
subplot (2,1,2); stem, (n, imag(x));
xlabel('Time index n');
ylabel('Amplitude');
title('Imaginary part');
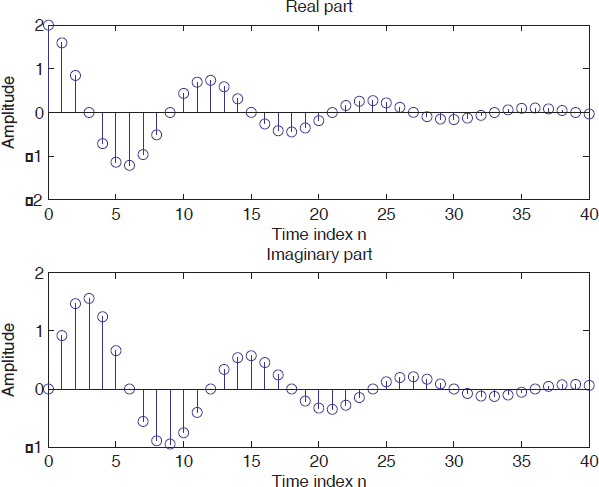
Figure 2.2. Real and imaginary parts of a complex discrete-time signal
K
Get Digital Signal Processing Using Matlab now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

