4.4. Equiripple filters and the Chebyshev approximation
4.4.1. Characteristics of the Chebyshev approximation
Butterworth filters are widely used, but their use has the drawback of an elevated degree of polynomials with standard applications. To get around this problem, an alternative solution consists in using equiripple filters and, more specifically, Chebyshev filters.
The type I Chebyshev approximation (or of type II or inverse) distributes the approximation error throughout the entire passband (or throughout the attenuated band). Unlike Butterworth filters, the frequency response curve then presents, with the Chebyshev approximation, an oscillation in this frequency band. This is an equal amplitude oscillation.
We should bear in mind that the maximum value of admissible error in relation to the reference level is minimized. Moreover, we can demonstrate that the amplitude in the attenuated band decreases in monotonically and much more quickly, for filters of an order above 1, than is the case with Butterworth filters.
4.4.2. Type I Chebyshev filters
4.4.2.1. The Chebyshev polynomial
We represent Cn(x), the Chebyshev function, sometimes called the Chebyshev polynomial, of order n as follows:
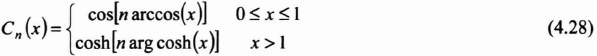
In Table 4.3, we give the Chebyshev functions of 0 to 4 for n. We see that these are even functions if n is even and odd functions if n is odd.
Figure 4.13. Variation curves of the first ...
Get Digital Filters Design for Signal and Image Processing now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

