4.3. Butterworth filters and the maximally flat approximation
4.3.1. Maximally flat functions (MFM)
Here we look at a low-pass normalized transfer function whose squared amplitude is shown in equation (4.3). We try to find a filter with the flattest possible frequency response in the passband when x is close to 0. To come as close as possible to the specification, the synthesized filter must have an amplitude diagram as flat as possible when x = 0. For that, we find the conditions that allow us to cancel the successive derivations of the function |H(jx)|2.
We know that the squared amplitude function |H(jx)|2, being analytic when x=0, can be developed by using the McLaurin series as follows:
![]()
This development introduces the successive derivatives of |H(jx)|2 used for x=0, or:
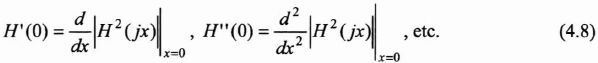
Moreover, |H(jx)|2 being a rational fraction (see equation (4.3)), we can approach it by a polynomial by proceeding to the division following increasing powers of polynomials that constitute the numerator and the denominator of |H(jx)|2. In this way we obtain the following development:
![]()
Since the McLaurin development is unique in the convergence region, we can then identify the coefficients of equations (4.7) and ...
Get Digital Filters Design for Signal and Image Processing now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

