Differential Equations Workbook For Dummies®

9.3. Working with Euler's Equation

NOTE

Solving Euler's equation allows you to find the solution to many differential equations with regular singular points. If you can put a differential equation into a similar form to Euler's equation, you can use a series expansion around the solutions you develop for Euler's equation. That's a pretty cool trick in my book.

When you want to play nice with Euler's equation, start by assuming a solution of this form: y = x^r.

Then substitute that solution into Euler's equation:

[r(r − 1) + αr + β] x^r = 0

r(r − 1) + αr + β = 0

r² − r + αr + β = 0

Ultimately, you wind up with

r² + (α − 1) r + β = 0

The roots, r₁ and r₂, of this equation are

You don't know what α and β are, so you're forced to consider three cases for these roots:

• r₁ and r₂ are real and distinct.

• r₁ and r₂ are real and equal.

• r₁ and r₂ are complex conjugates.

Following are examples to illustrate each of the three cases. When you're done reviewing them, get more acquainted with Euler's equation in the practice problems.

NOTE

EXAMPLE

Q. Solve this differential equation:

A. y = c₁x^1/2 + c₂x⁻¹

1. This differential equation has the form of Euler's equation:

   

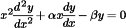
   which means you can assume its solution ...