8.8 MATRIX REPRESENTATION OF THE LFSR
In addition to the Berlekamp–Massey algorithm, there is another approach that will be useful to calculate the minimal polynomial p(z) = cN + cN−1z + ··· + c1zN − n + c0zN of an LFSR output sequence s0(0), s0(1), … when the length N of the LFSR is known. The forward recursion ![]() provides a relationship between consecutive N-blocks of LFSR output values:
provides a relationship between consecutive N-blocks of LFSR output values:
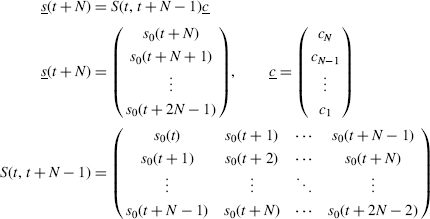
Proposition 8.8: If the LFSR has linear equivalence N, then
| 8.8a | The row of the N × N matrix S(t, t + N − 1) are linearly independent, and |
| 8.8b | The 2N consecutive outputs s0(t), s0(t + 1), …, s0(t + 2n − 1) determine the characteristic polynomial of the LFSR. |
Proof of (8.8a): If on the contrary, the rows of S are linearly dependent, there exists a vector d ≠ (0)N such that
![]()
This implies
![]()
Assuming without loss of generality that dN−1 = 1, we have
![]()
which contradicts the assumed linear equivalence.
Proof of (8.8b): Gaussian elimination and its application in cribbing Hill ...
Get Computer Security and Cryptography now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

