7.4 CRIBBING RED CIPHERTEXT
We will describe the cryptanalysis of RED ciphertext using English-language text. The vowel/consonant pattern of a (plaintext) crib u = (u0, u1, …, uM − 1) is
![]()
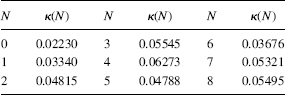
TABLE 7.8 Normalized κ-Values for Example 7.4
A necessary condition that the RED ciphertext fragment y[i,i+M) ≡ (yi,…, yi+M−1) be the encipherment of the (plaintext) crib u = (u0, u1, …, uM−1) is
![]()
To crib RED ciphertext for the plaintext u = (u0, u1, …, uM−1), the RED ciphertext is searched for fragments y[i,i+M) that have the same the vowel/consonant pattern as that of u.
Of course, Equation (7.17) is only a necessary condition that u → y[i,i+M) and some fragments fail to correspond to plaintext crib. Additional constraints need to be imposed before concluding that y[i,i+M) is the encipherment of the crib u.
7.4.1 Cribbing RED Cipherment: No Inactive Breakwheel Pins
If all pins on the breakwheel are active, then τ = 47 and P(i) = P(0) + i. As P(0) is unknown, the recovery of θV and θC by cryptanalysis assuming P(0) = 0 will then be related to Tables 7.5 and 7.6 by a shift in rows.
If y[i,i+M) = (yi, yi + 1, …, yi + M−1) is the RED encipherment of the crib u = (u0, u1, …, uM−1), then Equations (7.11 ...
Get Computer Security and Cryptography now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

