Computer Security and Cryptography

13.3 POLLARD'S p − 1 METHOD [POLLARD, 1974]

Find the prime factors of n

1. Choose an integer k that is a multiple of all integers less than some bound B; for example, k = B! or k = 1cm{1, 2, …, B}.
2. Randomly choose an integer a between 2 and n − 2.
3. Compute b = a^k (modulo n) and d = gcd{n, b − 1}.
4. If d is a trivial divisor of n, start over again with another choice of a and/or k.

TABLE 13.1 Example 13.1

TABLE 13.2 List of Primes ≤ 201

Example 13.2

n = 53,467, a = 3, k = 840 = 1cm{i :1 ≤ i ≤ 8}. See Tables 13.3 and 13.4.

Example 13.3

n = 34,163, a = 2, k = 840 = 1cm{i :1 ≤ i ≤ 8}. See Tables 13.5 and 13.6.

13.3.1 Explanation of Pollard's p − 1 Method

Let B be larger than any prime factor of p − 1 where p is a prime factor of n. If k is the least common multiple of all integers i with 1 ≤ i ≤ B, then by Fermat's Little Theorem, a^k = a^{C(p − 1)} = 1 (modulo p). This implies p divides both b − 1 = (a^k − 1) (modulo n) and n, ensuring that d = gcd{b − 1, n} is a nontrivial divisor of n.

Improved methods to factor require a diversion to review some number theory.

TABLE 13.3 Computing 34,944 = 3⁸⁴⁰ (modulo 53,467)

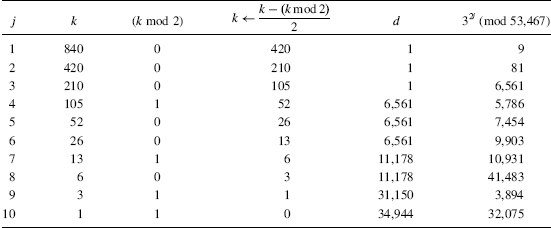
TABLE 13.4 Computing 421 = gcd{34,943, 53,467}

TABLE 13.5 Computing 16,892 = 2 ...