11.6 CRYPTANALYSIS OF THE MERKLE–HELLMAN KNAPSACK SYSTEM (MODULAR MAPPING) [SHAMIR, 1982]
UCSB has been the site of a meeting dealing with current topics in cryptography starting with CRYPTO ’81 in 1981. Adi Shamir electrified the attendees at CRYFTO ’82 by presenting an analysis of the Merkle–Hellman cryptosystem. A program running on an Apple during his lecture illustrated the solution technique that we now describe.
The mapping Tω−1,m: s = (s0, s1, …, sn−1) → a = (a0, a1, …, an−1) from the super-increasing to the public knapsack vector is nonlinear and this was the basis for believing that the Merkle–Hellman scheme provided a secure public-key encipherment scheme.
For ![]() define the modular mapping (function) ϕa,m(w) for 0 ≤ a, w < m (Fig. 11.1) by
define the modular mapping (function) ϕa,m(w) for 0 ≤ a, w < m (Fig. 11.1) by
![]()
- The continuous representation of the discrete-valued function ϕa,m(w) consists of straight-line segments with slope
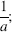
- ϕa, m (w) has minima nearly equal to 0 at the points
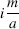 with i = 0, 1, …, a − 1; the distance between consecutive minima is larger than 1.
with i = 0, 1, …, a − 1; the distance between consecutive minima is larger than 1.
Write
Figure 11.1 The modular mapping function.
where kj is an integer <m. According ...
Get Computer Security and Cryptography now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

