Appendix C
MATLAB® Programs for Fuzzy Systems
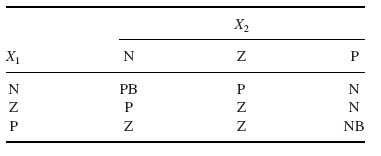
Example C.1.1 A system is described by two inputs (X1, X2) and a single output (Y) within the universes of discourse − 10 ≤ X1 ≤ 10, − 30 ≤ X2 ≤ 30 and − 20 ≤ Y ≤ 20, respectively. In order to develop a Mamdani-type fuzzy system, the membership functions for (X1, X2) and (Y) are defined in Figure C.1.1. The rule base for the Mamdani-type fuzzy system is given in Table C.1.1.
Figure C.1.1 Input and output membership functions. (a) Input membership functions; (b) Output membership function
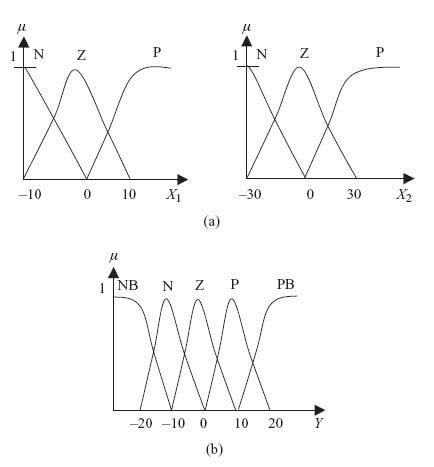
Table C.1.1 Rule base for a Mamdani-type system
A Mamdani-type fuzzy inference system for the above MFs and rule base is developed using MATLAB® and the Fuzzy Logic Toolbox.
%Fuzzy system − Example C.1.1 clear all;close all; sys=newfis('ExampleFS_1'); %-------------------------Inputs definition ----------------------------- %Define input variable X1 to FIS within interval [-10 10] sys=addvar(sys, 'input', 'X1', [-10 10]); %Define MFs N, Z and P for input X1 sys=addmf(sys, 'input', 1, 'N', 'trimf', [-10 -10 0]); sys=addmf(sys, 'input', 1, 'Z', 'trimf', [-10 0 10]); sys=addmf(sys, 'input', 1, 'P', 'trimf', [0 10 10]); %Define input variable X2 to FIS within interval [-30 30] sys=addvar(sys, 'input', 'X2', [-30 30]); %Define MFs N, Z and P for input ...Get Computational Intelligence: Synergies of Fuzzy Logic, Neural Networks and Evolutionary Computing now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

