Appendix C
Probability Theory
This appendix summarizes concepts from probability theory. This summary only concerns those concepts that are part of the mathematical background required for understanding this book. Mathematical peculiarities which are not relevant here are omitted. At the end of the appendix references to detailed treatments are given.
C.1 PROBABILITY THEORY AND RANDOM VARIABLES
The axiomatic development of probability involves the definitions of three concepts. Taken together these concepts are called an experiment. The three concepts are:
- (a) A set Ω consisting of outcomes ωi. A trial is the act of randomly drawing a single outcome. Hence, each trial produces one ω ∈ Ω.
- (b) A is a set of certain1 subsets of Ω.
Each subset α ∈ A is called an event. The event {ωi}, which consists of a single outcome, is called an elementary event. The set Ω is called the certain event. The empty subset
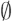 is called the impossible event. We say that an event α occurred if the outcome ω of a trial is contained in α, i.e. if ω ∈ α.
is called the impossible event. We say that an event α occurred if the outcome ω of a trial is contained in α, i.e. if ω ∈ α. - (c) A real function P(α) is defined on A. This function, called probability, satisfies the following axioms:
- I: P(α) ≥ 0
- II: P(Ω) = 1
- III: If α, β ∈ A and
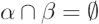 then P(α ∪ β) = P(α) + P(β)
then P(α ∪ β) = P(α) + P(β)
Example
The space of outcomes corresponding to the colours of a traffic-light ...
Get Classification, Parameter Estimation and State Estimation: An Engineering Approach Using MATLAB now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

