2.4 Overview of Multivariate Statistics
2.4.1 General Definitions
From a Bayesian viewpoint, a stochastic variable is a variable whose value is not fixed deterministically, but can vary according to a probability distribution. The stochastic variable is often multidimensional so that the underlying probability distribution is multivariate. In addition, the expected value of the stochastic variable can be time varying, with the change of the underlying distribution in time governed by some dynamic or transition equation.
2.4.1.1 Probability Density Function
We begin this section with a discussion of the general definitions of a probability density function (pdf) and a cumulative distribution function (cdf) for multidimensional stochastic variables.
A probability density function of a stochastic (random) multidimensional variable x at the point x = ξ is defined by [17]
(2.77) ![]()
where dξ is an infinitesimal interval. It follows immediately that the probability that x lies in the interval η ≤ x ≤ ξ is given by
(2.78) 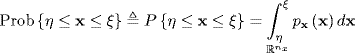
where nx is the dimension of x and the multidimensional integral is defined by
(2.79) 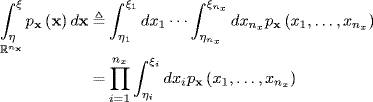
Thus, the probability that x lies in the interval η ≤ x ≤ ξ is the multidimensional “volume” ...
Get Bayesian Estimation and Tracking: A Practical Guide now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

