2
THE TRANSMISSION-LINE EQUATIONS FOR TWO-CONDUCTOR LINES
In this chapter, we will show the derivation of the transmission-line equations for two-conductor lines from two points of view. First, they will be derived from the integral form of Maxwell's equations, and second they will be derived from the per-unit-length distributed parameter equivalent circuit. Both methods allow the incorporation of conductor losses. In Chapter 3, we will repeat this for a general (n + 1)-conductor multiconductor transmission line (MTL). The process will be identical to that for a two-conductor line, but the details will be a bit more tedious. Nevertheless, the transmission-line equations for an MTL, written using matrix notation, will be identical in form to those for a two-conductor line.
2.1 DERIVATION OF THE TRANSMISSION-LINE EQUATIONS FROM THE INTEGRAL FORM OF MAXWELL'S EQUATIONS
Recall Faraday's law in integral form [A.1,A.6]:
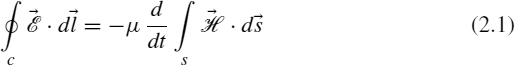
This is illustrated in Figure 2.1. The differential path length around the closed contour c that bounds the open surface s is denoted by ![]() . A differential surface area of surface s is denoted by
. A differential surface area of surface s is denoted by ![]() , where is a unit normal to the surface. The direction of the contour c and ...
, where is a unit normal to the surface. The direction of the contour c and ...
Get Analysis of Multiconductor Transmission Lines, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

