1
Combinatorics
Combinatorics deals with the cardinality of classes of objects. The first example that jumps to our minds is the computation of how many triplets can be drawn from 90 different balls. In this chapter and the next we are going to compute the cardinality of several classes of objects.
1.1 Binomial coefficients
1.1.1 Pascal triangle
Binomial coeffcients are defined as
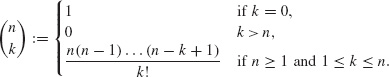
Binomial coefficients are usually grouped in an infinite matrix
![]()
called a Pascal triangle given the triangular arrangement of the nonzero entries, see Figure 1.1. Here and throughout the book we denote the entries of a matrix (finite or infinite) A = ![]() where the superscript i and the subscript j mean the ith row and the jth column, respectively. Notice that the entries of each row of C are zero if the column index is large enough,
where the superscript i and the subscript j mean the ith row and the jth column, respectively. Notice that the entries of each row of C are zero if the column index is large enough, ![]() , j with j > i ≥ 0. We also recall the Newton binomial formula,
, j with j > i ≥ 0. We also recall the Newton binomial formula,
![]()
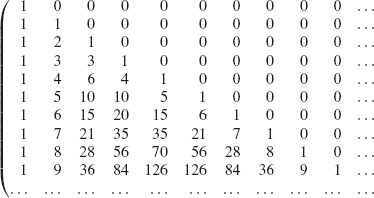
Figure 1.1 Pascal ...
Get A First Course in Probability and Markov Chains now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

