Appendix C
Systems of linear ordinary differential equations
We assume the reader is already familiar with first- and second-order linear ordinary differential equations (ODEs) with constant coefficients, either homogeneous or not. Here, we review results on the solutions to systems of N first-order linear ODEs.
C.1 Cauchy problem
We first consider the existence and uniqueness of a C1 solution X: [a, b] → ![]() to the problem
to the problem
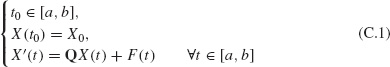
where ![]() is the given initial datum, Q is a given real N × N matrix and F : [a, b] →
is the given initial datum, Q is a given real N × N matrix and F : [a, b] → ![]() is a given continuous function.
is a given continuous function.
C.1.1 Uniqueness
Lemma C.1 (Grönwall) Let W ![]() C1(]a, b[,
C1(]a, b[, ![]() ) satisfy the inequality
) satisfy the inequality
![]()
for some α ≥ 0 and β > 0. Then
![]()
Proof. Let ∊ > 0. The function is strictly ...
Get A First Course in Probability and Markov Chains now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

